1. A végtelen és a kételemű számok

Korábban már kapcsolatot találtam a kételemű számok, és a végtelen egy speciális értelmezése között. Ezt kétféleképpen tettem meg:

1.1. A végtelenről másképp – heurisztikus megközelítéssel¹

A negatív számok gépi ábrázolása adta az ötletet, hogy a végtelen nagy számokat a valós tört számok helyiértékes számábrázolásához hasonlóan írjam fel, például egy speciális végtelen szám a következő helyiértékes alakban írható fel a tízes számrendszerben:

…999                                                               (1)

Azaz a …999 szám esetében megszámlálhatóan sok 9 szerepel az egész számok ábrázolására használt helyiértékeken a 10-es számrendszerben.

Mit tudunk elmondani erről a fenti végtelen nagy számról? Mindenekelőtt azt, amit a valós ’–1’-ről, azaz

…999²=1                                                         (2)

A fenti egyenlőséget az ember idegenkedve nézi, hiszen azt kaptuk, hogy egy végtelen nagy szám négyzete véges nagy. Ez hasonlóan értelmezhető, mint a gépi számítások során az un. túlcsordulás jelensége. Mondhatjuk, hogy a (2) egyenletet egy szorzáskor előfordult „túlcsordulás” magyarázza, mely akkor áll elő, ha a számábrázolás nem terjed ki az un. transzfinit – azaz minden természetes számnál nagyobb – helyiértékeken való számábrázolásra. Cantor fogalmait használva ez az a végtelen, amit 10^μ formában írhatok fel, ahol μ a természetes számok számossága, azaz olyan végtelen, melynek helyiértékes ábrázolásában a sorrendben 10^μ-dik helyiértéken értékes, azaz nem 0 számjegy áll. Ugyanakkor lehetnek olyan végtelen nagy számok, melyek minden természetes számnál nagyobbak, de kisebbek a transzfinit helyiértékeken is értékes – azaz nem 0 – számjegyeket is tartalmazó számoknál. Ezen számok egyike a (2) egyenletben megnevezett …999 szám is, tehát általában azok a számok, melyeknél a transzfinit helyiértéken lévő esetlegesen értékes számjegyekkel nem számolhatok, mert „nincs rá hely”, de tetszőlegesen nagy természetes számhoz tartozó helyiértéken van nem 0 számjegyük.

______________________________________________

¹ Az itt leírtakat „Az idő, a tér és a végtelen” című írásom 4.5 pontjából emeltem át

A teljes szöveg PDF fájlban itt található, Stefan Ulrych neve javítva 2017. július 6-án.

Levél BZ-nek

Kedves Z!

Ahogy olvasom, foglalkozol Kuhn paradigma-elméletével is. Ha látnád, hogy az én könyvem mennyire tele van firkálva megjegyzésekkel! (Mellesleg 1984-ben 44Ft volt ennek a könyvnek az ára. Hihetetlen! Ez 100-szoros árnövekedést jelent 30 év alatt!)

Bármennyire is nagyra tartom Thomas S. Kuhn könyvét a tudományos forradalmakról, azért nagyon sokban nem értek vele egyet, és tettem ezt már akkor is, amikor először olvastam. Talán érdekel, ezért összefoglalom az ellenérzéseimet vele kapcsolatban.

– Azt már szóban is említettem, hogy a paradigma-váltás fogalmával tulajdonképpen fölfedezte a spanyolviaszt, hiszen az nem más, mint a dialektikus materializmus mennyiség minőségbe csapásának törvényszerűsége és ennek alkalmazása a tudományok változására.
– Kritizálja Karl Poppert, aki a falszifikációs – azaz a cáfolhatósági – feltételt tartotta kulcsfontosságúnak egy tudományos elméletre vonatkozóan. Kuhn ezzel kapcsolatos kritikájából kitűnik, hogy nem érti a Popper által állítottak lényegét. A cáfolhatósági követelménynek (matematikai) logikai alapja van. Popper kezdetben nem szerette az igazság/hamisság fogalmakat azok igen homályos volta miatt, de később örömmel üdvözölte a zseniális matematikus-filozófus Alfred Tarski definícióját, miszerint "az igazság a tényeknek (vagy a valóságnak) való megfelelés". Popper átveszi Tarski igazság-elméletéből azt a következtetést is, hogy "az igazság létezik, de nincs kritériuma, a hamisságnak viszont van kritériuma”, azaz megkülönböztető jegye. Ezek alapján Popper így fogalmaz: „Az igazságot «szabályozó elvnek» nevezem, mert bár az igazságra nincs kritériumunk, a hamisságra számos kritériumunk van. A hamisságnak ezek a kritériumai nem mindig alkalmazhatók, de nagyon gyakran rájövünk, ha valami hamis. Ezért van az, hogy az igazság keresése kritikus keresés.” És ez a kritikus keresés épp azt jelenti, hogy minden tudományos elmélettel kapcsolatban az ellentmondásokat kell keresni. Ennek megfelelően egy elmélet csak egy cáfolási próbálkozás kudarcával erősödhet. Ez a megerősítés viszont nem jelenti az elmélet verifikálását, azaz igazolását. Szerintem Kuhn azért nem érti Popper falszifikációval kapcsolatos elgondolásait, mert nem ismeri, vagy nem érti azokat az alapokat – az igazság/hamisság definícióit, kritériumait – amelyen a cáfolhatósági posztulátum nyugszik.

– Nagy hibának tartom Kuhn leírásában azt, amilyen módon lebecsüli egy-egy paradigma-váltás után a részfeladatok aprólékos elvégzését a tudományokban. Első hallásra paradoxul hangzik, pedig igaz, hogy összességében információ-vesztéssel jár az új paradigma megjelenése, ugyanakkor a Kuhn által lekicsinyelt "utómunkálatok" során folyamatos információ-növekedés zajlik. Azért hangzik ez ellentmondásosan, mert az új paradigmában az új a hangsúlyos, és ez alatt valamilyen új információ megjelenésére gondolunk. Ez igaz, de ugyanakkor az új paradigmának a megjelenésével együtt rengeteg – és közöttük nagyon sok jó – elképzelés háttérbe szorul, elfelejtődik, törlődik. Jobban érthető az egész folyamat, ha a rendszer bonyolultság-változásával mérjük az információ-változást. Egy új paradigma megjelenése mindig egyszerűsödést jelent – ezt Kuhn is jól látja – az egyszerűsödés viszont azt jeleni, hogy a rendszer bonyolultsága csökken, azaz információ-tartalma csökken. Ezzel szemben, a paradigmaváltás utáni részfeladatok elvégzésével egyre nő a rendszer bonyolultsága, információtartalma. (Egyébként ezt a folyamatot sokkal részletesebben leírtam "A változásokról és az evolúcióról" című írásomban.)

No, ennyit dióhéjban. Kizárólag a legfontosabb kritikáimat emeltem ki Kuhn könyvével kapcsolatban, és remélem, hogy így nem is lett túl hosszú, és túl zavaros a magyarázatom.

Üdvözlettel,
K.

Vannak olyan problémák a geometriai algebra kialakulóban lévő használatában¹, amelyekre nem-igen tér ki a szakirodalom, ezekről szeretnék most néhány gondolatot felvetni. A vizsgálatomat leszűkítem azokra a geometriai algebrákra, ahol véges dimenziós Euklideszi vektortér és a valós számok teste a kiindulópont. Az Euklideszi vektortéren adottnak tekintek egy skaláris, vagy belső szorzatot, valamint a Grassmann által általánosított külső szorzatot, amit ˄‑szorzatnak is fogok nevezni. Ezek után egy úgynevezett geometriai szorzat kerül bevezetésre, mely a geometriai algebra alapművelete lesz.Ez a geometriai szorzat a két vektor belső és külső szorzatának összegével egyenlő. E szorzatot asszociatívnak deklarálják ahhoz hasonlóan, amint a Clifford algebra alapján a geometriai algebra legáltalánosabb, absztrakt, axiomatikus felépítésében teszik. A fent leírt esetben a szorzat asszociativitásának levezethetőségére láttam egy rossz példát Hestenes egyik könyvében, ahol épp a lényeg hiányzik, azaz a műveletek már definiált tulajdonságaiból az asszociativitás bizonyítása. A szerző csak a geometriai szorzat asszociativitásának elégségességét tudja bizonyítani a belső és a külső szorzat jól definiált tulajdonságaira vonatkozóan, a szükségességét viszont nem, tehát azt nem bizonyítja, hogy az alapműveletek tulajdonságaiból szükségszerűen következik a geometriai szorzat asszociativitása.

__________________________________________________________

¹ Lásd például Chris Doran - Anthony Lasenby könyvét: Geometric Algebra for Physicists;
http://www.cambridge.org/nl/academic/subjects/physics/theoretical-physics-and-mathematical-physics/geometric-algebra-physicists?format=PB
vagy Stephen Gull, Anthony Lasenby, Chris Doran korábbi cikkét, „Imaginary Numbers are not Real — the Geometric Algebra of Spacetime”;
http://geometry.mrao.cam.ac.uk/wp-content/uploads/2015/02/ImagNumbersArentReal.pdf , vagy másutt:

http://www.researchgate.net/publication/226188504_Imaginary_numbers_are_not_realThe_geometric_algebra_of_spacetime

Mai nappal töröltem az eredeti anyagot tartalmazó PDF fájlt, mert hibát találtam az egyik bizonyításban. A javítás folyamatban van, amint elkészül a teljes cikk; mellékelem. 2016. október. 5.

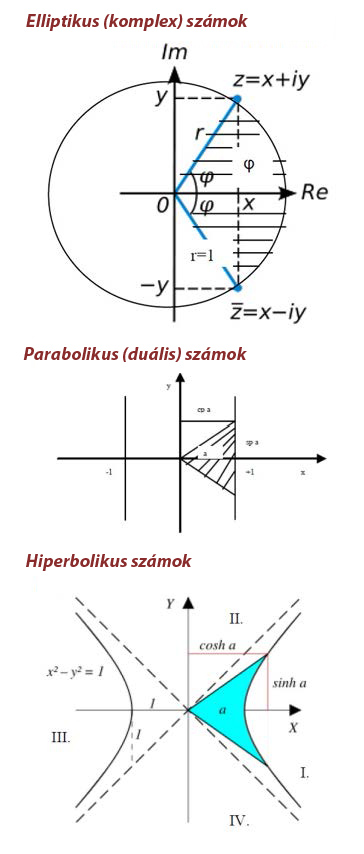Ebben a témában ott fejeztem be az előző írást, hogy jó lenne, ha a geometriai algebrában is hasonlóan kezelnénk a skalárokat, mint a kételemű számok¹ síkjain a valós számokat. A kételemű számok egyike, a hiperbolikus számok síkja a valódi téridőt modellezi, amennyiben a valós tengelyt az idő-tengelynek, a képzetes tengelyt egy tér-dimenziónak tekintjük.² Ebből a modellből következően logikus gondolat a valós számokat – azaz a skalárokat – a geometriai algebrában is „idő-szerűnek” tekinteni, és az Euklideszi vektortérre merőleges egyenesen ábrázolni. Így a valós számokra is vektorként tekinthetek, mégpedig olyan vektorként, mely merőleges az Euklideszi terem valamennyi térvektorára, bármit jelentsen is egyelőre ez a merőlegesség. Ha a merőlegességet a skalárszorzat eltűnésével definiáljuk, akkor az időtengely és az Euklideszi tér merőlegessége miatt a valósok és egy térvektor geometriai szorzata egy bivektor.

A skalárszorzat definíciója mindhárom – komplex, parabolikus és hiperbolikus – számsíkon azonosan fogalmazható meg, mégpedig egy számvektor konjugáltjának felhasználásával:³

__________________________________________

¹ A kételemű számokról egy rövid összefoglaló a Mellékletben található.

² Erről bővebben „Az idő, a tér és a végtelen” című cikkeben olvasható.

³ A részleteket lásd „A szimplektikus teve természetes előfordulásai” című cikkben.

A teljes szöveg PDF fájlban itt található.

Tartalom:

1. Láng Zsolt, Mircea Cărtărescu i-je

2. Lázár Balázs, Közben – A 80 éves Bertók Lászlónak

Könyvajánló

„Nem az a legfontosabb dolog, hogy vajon az olvasók Einstein fizikája, vagy Bergson filozófiája pártján állnak: ez a könyv olyan új gondolkodásmódot tár fel a tudomány és a humán területek közötti kapcsolatról, mely kizökkenti mindkettőt.”
/Gerald Holton, Harvard Egyetem/

Az idő-fogalom és a geometriai algebra

„Csak Grassmann külső szorzatának tükrében válik érthetővé, hogy milyen tényleges geometriai fontossága van a görögök körültekintő megkülönböztetésének a szám és a terjedelem között. Ez körülbelül megfelel a skalár és a vektor közötti különbségnek. Tulajdonképpen a görög terjedelmet úgy adták össze, mint skalárt, de úgy szorozták, mint vektort, így a terjedelmek szorzása a görögöknél magával hozza az irány és a dimenzió fogalmát, és Euklidesznek tökéletesen igaza volt, amikor ezeket megkülönböztette a görög számok (mostani skalárjaink) szorzásától.”
/David Hestenes, A klasszikus mechanika új alapjai/¹

1. Emlékeztető² a kételemű számokon definiált speciális szorzatokról

A kételemű számokon definiált skaláris, ferde skaláris, valamint geometriai szorzattal kapcsolatos egyenlőségek nem minden esetben egyeznek meg az axiomatikus geometriai algebrából ismertekkel. Ezek az eltérések nagyon tanulságosak, érdemes részletesen végignézni őket.

A teljes szöveg PDF fájlban itt található.

__________________________

¹„Only in the light of Grassmann’s outer product is it possible to understand that the careful Greek distinction between number and magnitude has real geometrical significance. It corresponds roughly to the distinction between scalar and vector. Actually the Greek magnitudes added like scalars but multiplied like vectors, so multiplication of Greek magnitudes involves the notions of direction and dimension, and Euclid was quite right in distinguishing it from multiplication of “Greek numbers” (our scalars).” /David Hestenes, New Foundations for Classical Mechanics/

² Lásd a „A szimplektikus teve természetes előfordulásai” és „A geometriai algebra alapelemei és a számok I.” című cikkeket.

Könyv előzetes

Az előző cikkemben említett Hestenes könyv mellett beszereztem a Doran-Lasenby szerzőpáros könyvét is a geometriai algebra – rövidítve GA – fizikai alkalmazásairól. Sokan és sokat dicsérték ezt a könyvet, mint a GA-t érthetően bemutatót és a GA sok fizikai alkalmazását tárgyaló gyűjteményt. Én ez utóbbira vagyok kíváncsi, mert Hestenes említett könyve csak egy szűk körét említi a fizikai alkalmazásoknak.

Még nem tudok véleményt formálni a könyvről, mert ezt is most kezdtem el olvasni Hestenes könyvével együtt. A könyv témáit illusztrálandó mellékeltem a könyv tartalomjegyzékét.

Könyv előzetes

David Hestenes egyik könyvéről tettem már korábban említést¹; „Clifford Algebra to Geometric Calculus – A Unified Language for Mathematics and Physics”, melynek társszerzője Garret Sobczyk. A régebben említett, és a címben most idézett könyv is a geometriai algebra – vagy, ahogy rövidítve emlegetik; GA – alapjainak bemutatásával kezdődik, de míg amaz a GA matematikai kifejtése, addig a címbeli a matematikai alapok bemutatása után az alkalmazásokra koncentrál a fizika néhány jelentős területén. A könyvről részletesebben nem tudok még szólni, mivel csak most szereztem be, és kezdtem el olvasni. A véleményem helyett álljon itt egy rövid részlet, a sok hozzászólásból, melyet az amazon.com-on olvastam: